(Pi): Facts and FiguresEdited by The Starman
(Pi): Facts and Figures
) to 100 decimal
places is:3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679
(Pi)
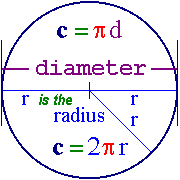 | is the ratio of a circle's circumference to its diameter (π = c / d) which also means that the
circumference of a circle is Pi times its diameter (c = πd) or twice Pi times its radius (c = 2πr). If we make the diameter 1 unit, then its
circumference will equal π units. The area (A) inside a circle is Pi times the radius squared or A = π r2 (see links below for
proof *). If a circle has a diameter of 2 units, then its area will equal π units squared; for example, a circle of 2 cm in diameter has
an area of π cm2. |
is the 16th letter of the Greek alphabet (it also denoted the number 80 in ancient Greece).
Note that the pronunciation of this letter in Greek is like the English word 'Pea' (the same way they say the name of the letter 'P') or
perhaps like the p and i in the word 'Pit.' But it's NEVER pronounced like the English word 'Pie' in Greece! To create that type of sound, Greek might use
the diphthong 'ai' (diphtong means two vowels together; like the 'oi' in the English word 'oil'); so, 'pai' in Greek might sound like 'pie' in
English.
So, how did this Greek letter become the Mathematical symbol it's known for today?
In the mid to late 1600's, some mathematicians were using 
(a lowercase Pi divided by a lowercase
Greek Delta) to note the perimeter divided by the diameter of a circle; 3.14159... . The symbol, π, was used in this manner because it's
the first letter of the Greek words, perifereia (periphery) and perimetroV (or perimeter; which could also mean the circumference of a circle). Many geometrical terms in
English come from Greek, including of course, geometry itself, gewmetria (gew = earth +
metria = measure).
But William Jones is often cited as being the first author to use the Greek letter π for this constant in his 1706 work, A New Introduction to
Mathematics.
A circle has the smallest perimeter length (its circumference) to area ratio
(for a given shape), which is: (2πr)/(πr2) = 2 / r.
Centuries ago when mathematicians were also philosophers,
because of this smallest ratio property, they considered the circle to be the 'perfect' two-dimensional shape.
Now, if we spin a circle around any one of its possible diameter lines, we bring everything up one dimension, and turn that
circle into a 3D sphere with the property that this 3D shape also has the smallest surface area to volume ratio (for a
given volume or radius); that ratio being 3 / r. Further below, we'll explain why the Surface Area of a sphere is 4πr2
and its volume is (4/3)πr3, but for now, take a look at how that ratio results in 3/r:
That's pretty cool, how the 2D ratio for the circle turned out to be 2/r, and the 3D ratio for the sphere was 3/r.
Another curious ratio is that of a sphere's surface area to the area of the circle we created it from, which is exactly 4: The surface area of a sphere being 4 times πr2 (the area of its circle).
There are some really nice and somewhat simple ways (compared to using Calculus) to show how the formulas for the Surface Area and Volume of a Sphere can
be derived!
The Volume is easier to show, if we simply assume for now that we have already proved the Surface Area, so let's start with that. Next, think of the
whole surface of a sphere as being made up of a huge number of little squares and that each of those squares is the bottom of a pyramid that has of course
as its height, the radius of the sphere. We will also assume here that the Volume of a Square Pyramid is one third (1/3) times its perpendicular height from
the middle of the Base times the Surface Area of that Square Base, or: (1/3) x BaseArea x height, or in the case of our Sphere: (1/3) x BA x r.
But, since the sum of all those tiny pyramids bases is equal to the Surface Area of the Sphere, then its Volume would be equal to: (r/3) x Surface Area =
(r/3) x 4πr2 = (4/3)πr3.
We have, of course, ignored the fact that each of those little "square pryamids" would have a slightly upward curved base that is not exactly a completely flat square! But the smaller we make those bases, the flatter that tiny square becomes and we arrive at values where it makes no practical difference. So that's why we have simply showed you a way to arrive at the formula, rather than having actually proved what it is; which can only be done using the principles of Calculus.
The formula for the Surface Area of a Sphere can be shown as follows:
Rather than take the time (I'm getting way too little sleep already!),
There's a nice presentation of this formula here, or watch
This VIDEO.
|
The following lists the repeating decimal portion (underlined) of the fractions above:
333/106 = 3 + (15/106 = 0.141509433962264)
355/113 = 3 +
(16/113 = 0.14159292035398230088495575221238938053097345132743
36283185840707964601769911504424778761061946902654
867256637168)
4703/33215 = 0.1415926539214210447087159
37741629/266550757 =
0.14159265358980015952458915732886100938741659623198
89416033434862839275297950101113387571433533764077
81126654237939380528564771624340200241862378203637
96603286330190388466989047042923986143472104264179
59863456699918507453347806474246854230468383175516
54899258080141186768417243699668052340215263391654
89595664513532032475150689592676714851723343633197
78529085175323662652363054440697011413852409355566
00201289242633814767218987864288826611736090473755
43562984516303587162575569050062761592532262063693
9327,
and even more digits before finally repeating!
The Babylonians were the first to use (25 / 8)
The fraction (22 / 7) is probably the most famous approximation for Pi (about 3.142857). It's actually composed of 3 + (1 / 7) and the fractional part (1/7) is famous in its own right as being the first fraction to produce a 'repeating decimal' number with more than a single digit! (1/7 = 0.142857 142857 142857 ... etc.)
(355 / 113) is about 3.141592920354 and only 0.00 00 0849% larger than Pi.
If one were to find the circumference of a circle the size of the known universe, requiring that the circumference be accurate to within the radius of one proton only 39 decimal places of Pi would be necessary!
The Babylonians are credited as having recorded the first value for Pi (around 2000 BCE) and they used (25/8).
The earliest known reference to Pi is on a Middle Kingdom papyrus scroll, written around 1650 BC by Ahmes the scribe.
In around 200 BC Archimedes found that Pi was between (223/71) and (22/7). His error was no more than 0.008227 %. He did this by approximating a circle as a 96 sided polygon.
Ludolph Van Ceulen (1540 - 1610), Germany, spent most of his life working out Pi to 35 decimal places, thus the reason, Pi is sometimes known there as Ludolph's Constant (in German: die Ludolphsche Zahl).
In 1706 (a fruitful year for Pi), Machin found this rapidly converging formula for its calculation:
π/4 = [4 x arctan (1/5)] - arctan (1/239).
Also in 1706, the Welshman, William Jones, became the first person to use the Greek letter π as an abbreviation for the periphery of a circle with
unit diameter. Euler adopted the symbol, and it quickly became the standard notation for Pi in all mathematical contexts.
In 1768 (or 1761), Johann H. Lambert proved Pi is irrational. An irrational number is a number that cannot be expressed in the form (a / b) where a and b are integers. Some other famous irrational numbers include the square root of 2 (the square root of any prime number is irrational) and e.
In 1882 Ferdinand Lindemann, proved the transcendence of Pi.
Transcendental in mathematics can mean: Not capable of being determined by any combination of a finite number of equations with rational integral coefficients. Another way of stating a number is 'transcendental' is to say it can never be the solution to any finite polynomial (that is, lots of numbers added in a series) with whole number coefficients. This is why it is impossible to "square the circle".
It is easy to prove that if you have a circle that fits exactly inside a square, then π = 4 x [(Area of circle) / (Area of square)] because each side
of the square is equal to the diameter of the circle, or 2 times the radius:
π = 4 x [ (πr2) / (side2) ] = 4 x [(πr2)/(4r2)] = (πr2)/(r2) = π.