The following equations are found on a single sheet included in the notes Samuel Herrick made for his work on the film,[1] The Day the Earth Stood Still (1951). I have placed a number [in brackets] next to each of them, so I can refer to specific ones on my page concerning all of the equations on the blackboard in that film. Included in Samuel Herrick's papers, was a little note that reads: “See D 19 J for why of what went on Barnhardt's blackboard.” Unfortuantely, no one at the university[1] has been able to find anything with that designation, and I was told it might have never even made it into the collection! So, this sheet is the best additional supplement we have from Herrick for understanding some of what's on the board. Again, note that the "[n]" bracketed numbers were added by me:
[01] \(\displaystyle \dot{r}=\frac{\sqrt{-a}}{r} C sinhF\) [02] \(\displaystyle C=1+\frac{9}{8}m\ a^3\ M^2\) [03] \(\displaystyle \dot{C} = \frac{9}{4}m\ a^3\ M\ \dot{M} \)
The \(\dot{r}\) would mean taking the first order differential of r, but with respect to what? (I can only assume a time t for now, so: \(dr/dt\)) Likewise for \(\dot{C}\) and \(\dot{M}\), and \(\dot{F}\) in [04].
[04] \(\displaystyle \ddot{r}=\ - \frac{\dot{r}\sqrt{-a}}{r^2}CsinhF + \frac{\sqrt{-a}}{r}C\dot{F}coshF + \frac{\sqrt{-a}}{r}\dot{C}sinhF\) (where \(\ddot{r}\) is a second order differential of r).
[05] \(\displaystyle \dot{M} = \frac{1}{(-a)^{3/2}}\)
[06] \(\displaystyle sinhF - F = M + \frac{3}{8}m\ a^3\ M^3 \)
[07] \(\displaystyle \frac{r}{-a}\ \dot{F} = C\dot{M}\) [08] \(\displaystyle \dot{F} = \frac{-a}{r}C\dot{M} = \frac{C}{r\sqrt{-a}}\) [09] \(\displaystyle \dot{C} = - \frac{9}{4}\ m(-a)^{3/2}\ M\)
[10] \(\displaystyle \ddot{r} = \frac{9}{r^3}\ C^2\ sinh^2F + \frac{C^2}{r^2}\ coshF - \frac{9m\ a^2\ M\ sinhF}{4r}\)
\(\displaystyle = \frac{9C^2}{r^3}\ (sinh^2F + coshF - cosh^2F)\ - \) " "
\(\displaystyle = - \frac{1}{r^2}\ C^2 - \frac{9m\ a^2\ M\ sinhF}{4r}\)
\(\displaystyle = - \frac{1}{r^2}\ - \frac{9m\ a^2\ M}{4r^2}\ (aM + r\ sinhF) \)
\((a\ sinhF - aF + a\ sin\ ....\) (what is this about?)
[11] \(\displaystyle M = sinhF - F = \frac{F^3}{6} +\ ...\)
[12] \(\displaystyle \frac{r}{a} = 1 - coshF = - \frac{F^2}{2} +\ ... \)
[13] \(\displaystyle F = \sqrt{\frac{2r}{-a}} \)
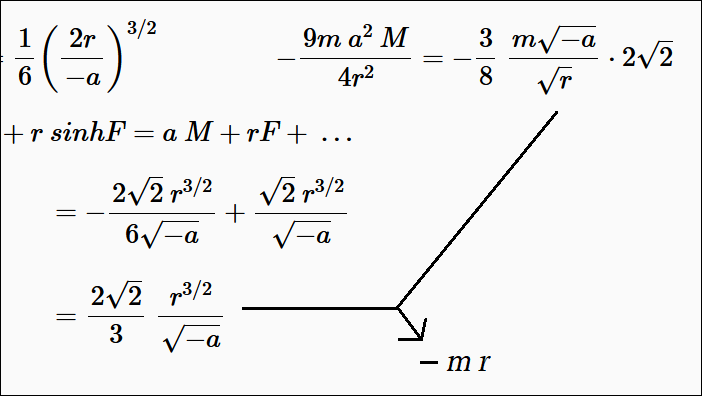
[14] \(\displaystyle M = \frac{1}{6}\left(\frac{2r}{-a}\right)^{3/2}\) [15] \(\displaystyle -\frac{9m\ a^2\ M}{4r^2} = -\frac{3}{8}\ \frac{m\sqrt{-a}}{\sqrt{r}}\cdot2\sqrt{2} \)
[16] \( a\ M + r\ sinhF = a\ M + rF +\ ... \)
\(\displaystyle = - \frac{2\sqrt{2}\ r^{3/2}}{6\sqrt{-a}} + \frac{\sqrt{2}\ r^{3/2}}{\sqrt{-a}} \)
\(\displaystyle = \frac{2\sqrt{2}}{3}\ \frac{r^{3/2}}{\sqrt{-a}} \) Note: At this
point, Herrick had drawn some lines on the paper: One coming down from the middle of the right-side of equation [15], another horizontally from here and a third with an arrowhead
pointing to: \(- mr\) (implying some kind of simplification could be made between them). Here's a diagram I made showing that:
Vertically, along the right edge of the sheet, Herrick had also written below "20-C-Fox": \(k^2\) and then somewhat below that \(cgs\), but below that he wrote out what is the Gravitational Constant: \(\left(6.670 \pm 0.005\right)\times10^{-8} \) in cgs units (centimeter, gram, second). Most often today, this constant is given as: \(6.6743 \times 10^{-11}\ m^3\ kg^{-1}\ s^{-2}\) in mks units (meter, kilogram, second). But, Herrick crossed it out. So, we really don't know for sure why he wrote it; maybe just trying to recall it for himself. After that we find: "B, A7" but I have no idea why.
Footnotes
1[Return to Text] This sheet can be found in Box 2, Folder 2 (B02F02) of the Samuel Herrick Papers (Ms1978-002), Special Collections and University Archives, University Libraries, Virginia Polytechnic Institute and State University. Note: You can view many of the equations on this page in the following video at timestamp 1:02:20 which I have cued the link to: Archival Adventures - Episode 81: Samuel Herrick Papers (Ms1978-002) (But not all are shown there).
First Posted on: 22 July 2025 (2025.07.22).